两个平面相互垂直 直线与平面垂直的判定微课

在几何学的世界里，平面是基础而常见的概念，而“平面垂直”则是一个充满力量与对立的数学关系。当两个平面相互垂直时，它们在空间中的交汇方式显得尤为独特和引人深思。为什么平面垂直如此重要？它不仅仅是一个抽象的数学概念，更是物理、工程、建筑等领域中至关重要的基本原理之一。我们将深入探讨平面垂直的几何含义、应用及其在实际生活中的关键作用。

平面垂直的几何定义

在三维空间中，两个平面垂直的定义非常简单：若两个平面之间的法向量相互垂直，则这两个平面是垂直的。换句话说，如果我们有两个平面

P_1

和

P_2

，它们的法向量分别为

\mathbf{n_1}

和

\mathbf{n_2}

，若这两个法向量满足

\mathbf{n_1} \cdot \mathbf{n_2} = 0

，那么

P_1

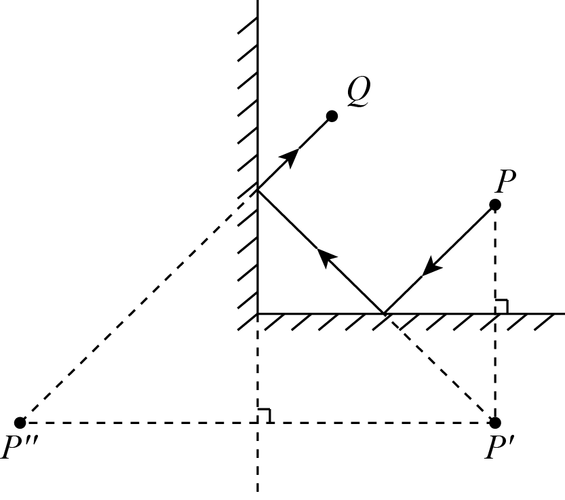
三个垂直的平面交线相互垂直

和

P_2

就是垂直的。法向量的点积为零，意味着这两个向量之间的夹角为 90 度，从而确定了平面间的垂直关系。

平面垂直的数学重要性

平面垂直在几何学中具有重要的理论地位。平面垂直关系为解决空间几何问题提供了简洁有效的工具。许多几何定理和公式都依赖于平面垂直的特性。例如，在计算平面之间的角度或距离时，垂直关系能够帮助简化复杂的计算过程。平面垂直的概念还广泛应用于矢量空间中的正交性问题。正交化方法——尤其是格拉姆-施密特正交化——利用了平面和向量之间的垂直关系，帮助我们将复杂的高维空间问题简化为更易于处理的一维或二维问题。

平面垂直在物理与工程中的应用

平面垂直不仅仅存在于抽象的数学世界，它在物理学、工程学等领域中同样具有重要的应用价值。例如，在建筑设计中，垂直的平面关系决定了建筑物各部分的稳定性和安全性。许多建筑结构的支撑系统和框架设计，都基于平面间垂直的原理，确保结构能够均匀分配重量，避免偏斜和不稳定。

在机械工程中，两个平面相互垂直的关系常常出现在机器零部件的制造和装配过程中。比如，齿轮系统中的齿面必须精确地垂直接触才能实现理想的传动效果。若齿轮齿面之间的夹角发生偏差，则会导致摩擦增加、效率降低，甚至可能造成系统损坏。平面垂直在制造精度中的作用不可小觑。

平面垂直在日常生活中的微妙影响

或许你并未意识到，平面垂直的概念已经渗透到日常生活的各个角落。例如，当你使用一把水平仪检查墙壁是否垂直时，其实是在利用平面垂直的原理来确保墙面与地面之间形成了90度的直角。又比如，在我们的计算机屏幕和桌面之间，虽然我们没有明确地去考虑，但平面垂直关系却悄然影响着显示效果的清晰度和观看的舒适度。

光学镜头的设计、汽车轮胎与地面的接触面、甚至摄影中的视角控制等方面，平面垂直的应用无处不在。它不仅仅是几何抽象的数学工具，它是支撑我们日常生活和工业生产的隐形力量。

平面垂直的多维价值

平面垂直是几何学中一个简单而深刻的概念，它在数学、物理、工程乃至日常生活中都有着广泛的应用。从数学角度看，平面垂直提供了我们理解空间关系的基础框架；在工程设计中，平面垂直是确保结构稳定和功能有效的关键因素；而在日常生活中，我们无时无刻不在依赖平面垂直所带来的精确和舒适。通过对平面垂直这一概念的深入理解，我们能够更好地掌控空间、设计出更加完美和高效的系统。

无论是学习几何学的学生，还是在实际工作中应用这些原理的工程师，平面垂直都是一个值得关注的核心概念。它不仅仅存在于课本中，更是推动科技和社会进步的重要力量。